Hoy os voy a contar el segundo método. Este fue el que utilicé hace dos años y los problemas eran los mismos. Si con este curso decidí no utilizarlo es porque mezcla la suma con la resta.
Aquí os dejo los pasos que se siguen con este método.
Método 2
1. Al igual que en el anterior, explica que el número de arriba es el minuendo y siempre tiene que ser el de mayor cantidad. Entre el 32 y el 17, elegiríamos como minuendo el 32.
2. A continuación, empezaremos a realizar la resta, y recuerda, siempre por la derecha, por la columna de las unidades. Cuando la unidad del minuendo es menor (en este caso 2 < 7), tendremos que pedir ayuda a la columna de las decenas.
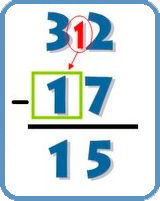
3. A la columna de las decenas, le pedimos 1, convirtiendo así el 2 en un 12. Y efectuaremos la resta de las unidades: – De 7 a 12 van 5. Y lo escribo.
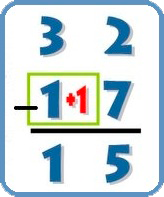
4. Para el siguiente paso, al contrario que en el método 1, sumamos uno a la decena de abajo (aquí es donde entra la suma).
5. Quedando en la columna de las decenas 3 – 2. Y ya podremos hacer la resta de las decenas: – De 2 a 3 va 1. Y lo escribo.
6. Después de este paso, habré terminado mi resta. Siendo el resultado 15. En el caso de que fuera una resta con decenas, repetiríamos los pasos 3 y 4.
Seguramente este sea el método que usáis la mayoría y que puede que yo vuelva a utilizar al año que viene.
En muchas ocasiones, y si la organización del centro lo permite, utilizareis el mismo método en el nivel. El problema viene cuando llegas a Segundo, en tu clase hay un niño que repite y su profesora del año pasado le enseñó con otro método. ¿Qué haces en ese caso?
Bueno, si los/as profes se enteran del método, perfecto, yo seguiré tirando de calculadora 😉
Puede que quede algo lioso, y es cierto que cuando se lo explicamos a los padres en la reunión general se quedan con la boca abierta, pero para que la resta llegue a ser algo mecánico hay que empezar por aquí. 😀
Desde el punto de vista lógico y matemático este modo me parece totalmente incorrecto. Es que no tiene explicación lógica. No puede ser que pidiéndole uno a las desenas del sustrayendo la cifra se queda igual, lo lógico es que después de prestar una desena, siguiendo el ejemplo la cifra de decenas se quedaría en 0. Este método da lugar a muchos errores porque es totalmente incompatible con la lógica. ¿Y qué pasa si la cifra de las decenas es cero? ¿Nos sacamos una decena de la manga?
El método correcto para primaria es el uno y de esta forma además de aprender a restar correctamente reforzamos las posiciones de las cifras en un número. Lo lógico y correcto es que si te faltan unidades para hacer la resta te prestan las desenas y como es lógico queda un decena menos (por esto antes debes de saber que una decena son 10 unidades), si nos faltan decenas pedimos a las centenas y nos queda una centena menos (para hacerlo de forma correcta debemos saber de una centena son 10 decenas), etc. Esto si es matemática y el otro son trucos por si algún alumno se queda atascado para sacarlo del apurado.
Con el Método 2 sí que se obtiene un resultado correcto pero la forma de llegar a este resultado es totalmente incorrecta desde el punto de vista matemático. Dudo mucho que algún profesor de Segundaria aplique este método.
Gracias por tu opinión Bory! La tendré muy en cuenta, otra vez, estoy con las restas con llevada en clase!!