En 1970 se dieron cuenta de que si querían que desapareciera el analfabetismo general que existía o la gran tasa de abandono escolar (casi de un 60 %) debían invertir en educación. Y así lo hicieron. Dieron prioridad a la idea de cambiar la forma matemática y científica de pensar para facilitar la transformación económica y educativa que necesitaban para sobrevivir; creando ciudadanos innovadores que tuvieran la posibilidad de visualizar diferentes caminos para resolver un problema no solo matemático, también problemas de la vida diaria.
Realizaron estudios científicos y a partir de 1980 empieza el gran cambio ¡Solo 15 años después! Al principio se centraron en el aprendizaje de conceptos y resolución de problemas, años después desarrollaron distintas formas de pensamiento, realizando actividades matemáticas en grupo y de resolución de problemas.
A día de hoy, Singapur ocupa el 1º puesto en el Informe PISA, siendo en el área de matemáticas donde la diferencia respecto a las otras áreas y otros países es mayor.
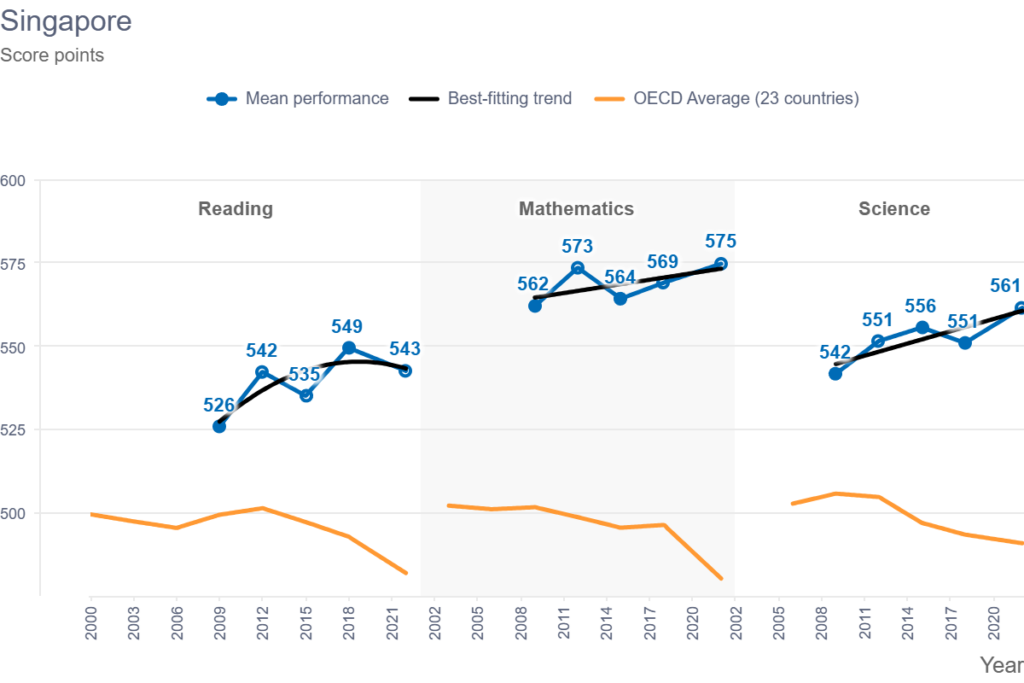
Fuente: OECD, PISA 2022 Database, Tables I.B1.5.4, I.B1.5.5 and I.B1.5.6.
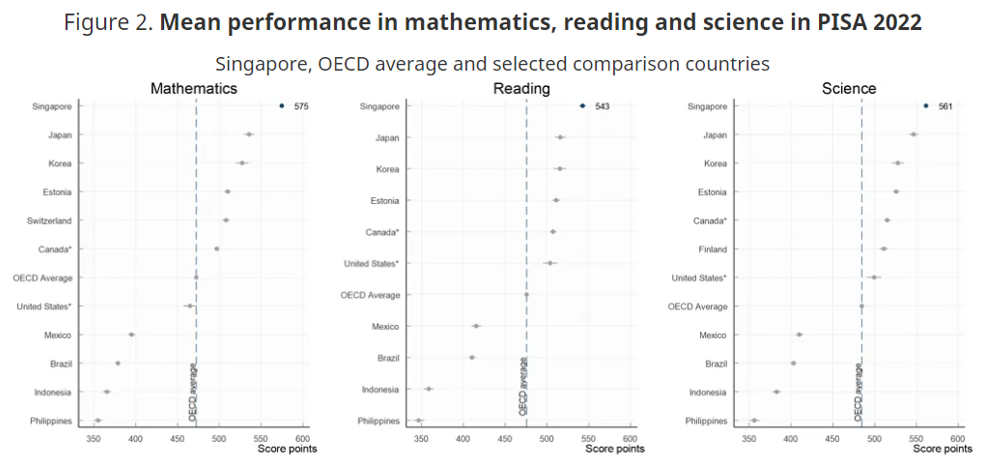
Fuente: OECD, PISA 2022 Database, Tables I.B1.2.1, I.B1.2.2 and I.B1.2.3.
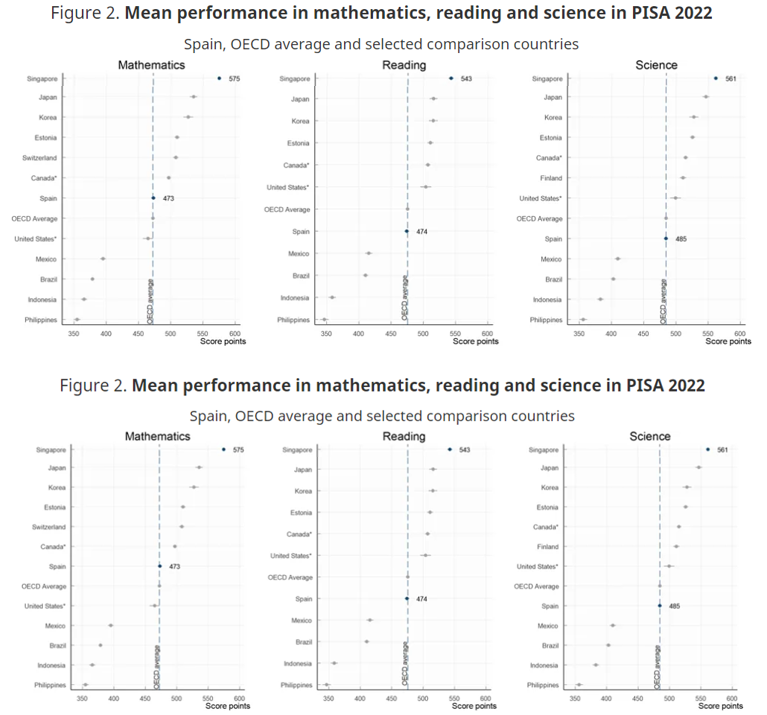
Fuente: https://www.oecd.org/publication/pisa-2022-results/country-notes/spain-f1a3afc1/
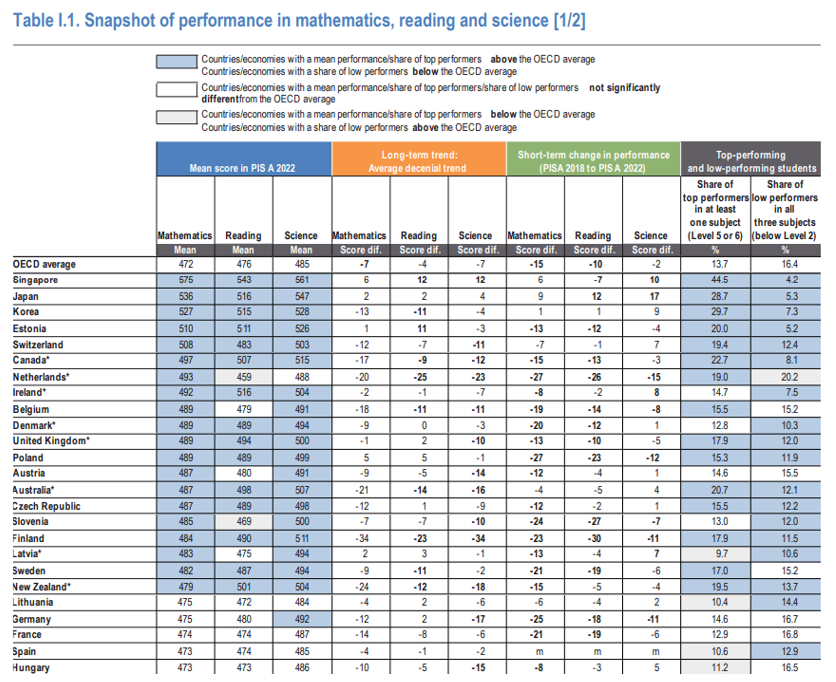
Veamos cuáles son sus fundamentos metodológicos y a qué grandes pedagogos pidieron ayuda para llegar hasta aquí.
Fundamentos Metodológicos del Método Singapur
– El aprendizaje en 3 etapas: CPA (Concreto – Pictórico – Abstracto) Empezaremos a trabajar desde algo concreto, que después representaremos de forma pictórica para en último lugar entender de forma abstracta.
– La superación de la dicotomía para trabajar en paralelo: La comprensión de conceptos y el aprendizaje de procedimientos, serán el camino que descubrirán nuestros estudiantes.
– Variedad en las presentaciones. La comprensión de un concepto es mejor si lo hacemos de varias formas, por ello, en lugar de ponerles 4 sumas iguales, les diremos que resuelvan una suma de todas las formas que puedan (usando la recta numérica, los números conectados, la suma en vertical,…)
– El andamiaje y la zona de desarrollo próximo. La mejor forma de aprender es en grupo, cualquier solución correcta o incorrecta se debate. Y después es acompañada por el adulto, por la persona con conocimientos, que en ningún caso les dirá que la solución a la que han llegado es incorrecta, sino que les animará a seguir probando y buscando otras formas de trabajar, consiguiendo así que el alumno o la alumna sea el protagonista de su propio aprendizaje.
Pedagogos en los que se basa el método
- Jerome Bruner, psicólogo, profesor y pedagogo estadounidense. Decía que hemos nacido con cerebros visuales, por eso trabajó el CPA. Jerome creía en la relación que existe desde lo concreto hasta lo abstracto, pasando por lo pictórico. Por eso usamos material manipulativo en el Método Singapur. Material como el que creó nuestro segundo autor.
- Zoltan Dienes, matemático húngaro. Zoltan le da un enfoque diferente del aprendizaje de las matemáticas utilizando juegos, canciones y bailes para hacerlo más atractivo a niñas y niños. Se le atribuye la creación de los Bloques en base 10, popularmente conocidos como los «Bloques lógicos de Dienes». Material manipulativo básico para este método.
- Richard Skemp, educador inglés. Skemp estudió los aspectos psicológicos del aprendizaje de las matemáticas centrando sus ideas en la comprensión y en la formación de conceptos. El lenguaje formal no lo podemos usar directamente con los alumnos, debemos usar los conceptos para que entiendan que unos conceptos derivan de otros: sumas, sumas de iguales…multiplicación. Los alumnos necesitan un tiempo para interiorizar las ideas. Los alumnos van construyendo el contenido con sus palabras.
- Lev Vygotsky, psicólogo ruso. Vygotsky señalaba que la inteligencia se desarrolla gracias a ciertos instrumentos o herramientas psicológicas que el niño encuentra en su medio ambiente (entorno), entre los que el lenguaje se considera la herramienta fundamental, por ello pensaba que la mejor forma de aprender es siempre en grupo y por ello en este método es tan importante el trabajo en equipo.
Curriculum Singapur
Ahora quiero que os imaginéis una casita de perro, que penséis en un pentágono.
Los cimientos de esta casa serán los conceptos (Numéricos, algebraicos, geométricos, estadísticos, probabilidad y conceptos analíticos…). Tenemos que saber de dónde partir y qué queremos conseguir.
Las paredes serán los procesos y las habilidades. Las habilidades matemáticas como el cálculo numérico, la visualización espacial, la manipulación algebraica, el análisis de datos, la estimación, o el uso de herramientas. Y el proceso, donde encontraremos el razonamiento, las conexiones, la comunicación, las aplicaciones y las habilidades entre otros. Aspectos muy importantes para el desarrollo del aprendizaje de las matemáticas.
Y el techo. Aquí se tendrán en cuenta cosas como la actitud de los profes y los alumnos (interés, perseverancia, esfuerzo y disfrute de las mates) y la metacognición (ser conscientes de los propios procesos de pensamiento y habilidad de controlarlos: sobre todo para la resolución de matemáticas).
Un día usando el Método Singapur en el aula.
Y después de tanta teoría, y ya sabiendo de dónde viene las Matemáticas Singapur y qué queremos conseguir con ellas, bajemos al aula y veamos cómo se desarrolla una sesión en el aula.
Las sesiones de matemáticas suelen ser de una hora.
Siempre iniciamos la clase planteando un problema al alumnado, a este tiempo lo llamamos Exploramos, porque en grupos, los estudiantes buscan la forma de resolver el reto que se les plantea. Los estudiantes estarán en asamblea, les daremos un tiempo para que piensen individualmente cómo resolver el reto y por parejas lo podrán en común. Pasados unos minutos y después de haberles dejado que representen sus respuestas con material manipulativo o de forma pictórica en pizarras o folios, se expresarán en voz alta con sus propias palabras, contándoles a toda la clase cómo han resuelto el problema planteado. En ese momento el profesor registrará todos los métodos en la pizarra, al alcance de todos.

Pizarra 2º primaria en el Colegio Escuelas Pías Alcalá
La segunda parte de la clase, la llamaremos Aprendemos. Aquí dejaremos a los estudiantes que sean ellos mismos los que lean las distintas opciones de resolución del problema que teníamos, para que así pueda ver y aprender el lenguaje matemático. Es el momento, en el que como docente se deben aclarar posibles conceptos erróneos y sobre todo felicitar a los equipos, los problemas suelen ser resueltos de más de 3 formas diferentes y de forma correcta.
En la parte del Practicamos, la tercera parte de la clase, los niños y niñas trabajan en parejas o tríos para resolver los problemas que se proponen en las actividades del día. En las mesas estarán los materiales disponibles para aquellos alumnos que los necesiten. Y éste será el mejor momento de atender a los que tienen bajos y altos niveles de logro que se han detectado durante el tiempo de Exploramos.
Para terminar, el Trabajo Individual. Aquí los estudiantes deben tener un momento de trabajo individual en el que se enfrenten solos a los problemas del cuaderno de trabajo, y así comprobar si lo han entendido. Esta parte la podremos completar con el Diario de Aprendizaje. ¿Para qué este diario en el área de matemáticas? Entre otras y dependiendo del curso en el que estemos: Para interiorizar contenidos, reforzar o ampliar lo trabajado, para desarrollar su imaginación y creatividad. Incluso para poder documentar su proceso de aprendizaje.
Las familias y el Método Singapur en casa
Este es el punto en el que más he trabajado durante estos últimos años, respecto a otras asignaturas. Trabajar el método Singapur en clase es importante, pero que se pueda seguir trabajando en casa y que las familias lo respeten, es otro tema. Para ello, creé una formación online, a través de vídeos subidos a YouTube, explicando paso a paso como trabajarlo. Así las familias tendrían un sitio donde poder acudir. Aunque yo siempre les decía que sus hijos eran los profes y que ellos eran los que les iban a explicar las matemáticas a partir de ahora.
Para que todo tuviera un hilo conductor y con la idea de motivar a mis estudiantes, creé dos gamificaciones online, una para primero de primaria y otra para segundo de primaria. Ahí podréis encontrar juegos online, fichas, material manipulativo online y fotocopiable y vídeos tutoriales.
En este blog, UnaProfe.com encontraréis más recursos, y en mi Proyecto Colaborativo CuentaMates, cuentos escritos por y para trabajar este método desde el área de matemáticas.
Además, os recomiendo seguir a Luis Solano y su canal de YouTube Merlion Maths dedicado al método.
Y otros docentes como Belén Palop y Pedro Ramos en español y Yeap Ban Har en inglés.
Espero que os haya gustado y ayudado a conocer un poquito más, de qué va esta metodología matemática.






















