Este campo de las matemáticas me apasiona. Igual es porque en el instituto adoraba el Dibujo Técnico y quería ser arquitecta,..quién sabe.
La geometría estudia las propiedades de las figuras en el plano o el espacio. Hoy os vengo a hablar de las figuras en el espacio, de las figuras en tres dimensiones, de los cuerpos geométricos.
Su conocimiento nos ayudará a la resolución de problemas concretos relativos a medidas, utilizados en arquitectura, geografía, astronomía,… y nos será útil en la preparación de diseños e incluso en la fabricación de artesanía.
A los cuerpos geométricos también los llamamos figuras de tres dimensiones, 3D. Eso que aprendimos todos a diferenciar con la primera película 3D que vimos en el cine…jajajaja.
Tipos de cuerpos geométricos
Existen varias clases de cuerpos geométricos, a mi me gusta hacer dos grandes clasificaciones: Los que tienes alguna superficie curva y los que tienes todas las caras planas.
Aunque hablaremos también del primer grupo, en esta entrada me centraré en los segundo, en aquellos que tienen todas sus caras planas.
Cuerpos geométricos con alguna superficie curva
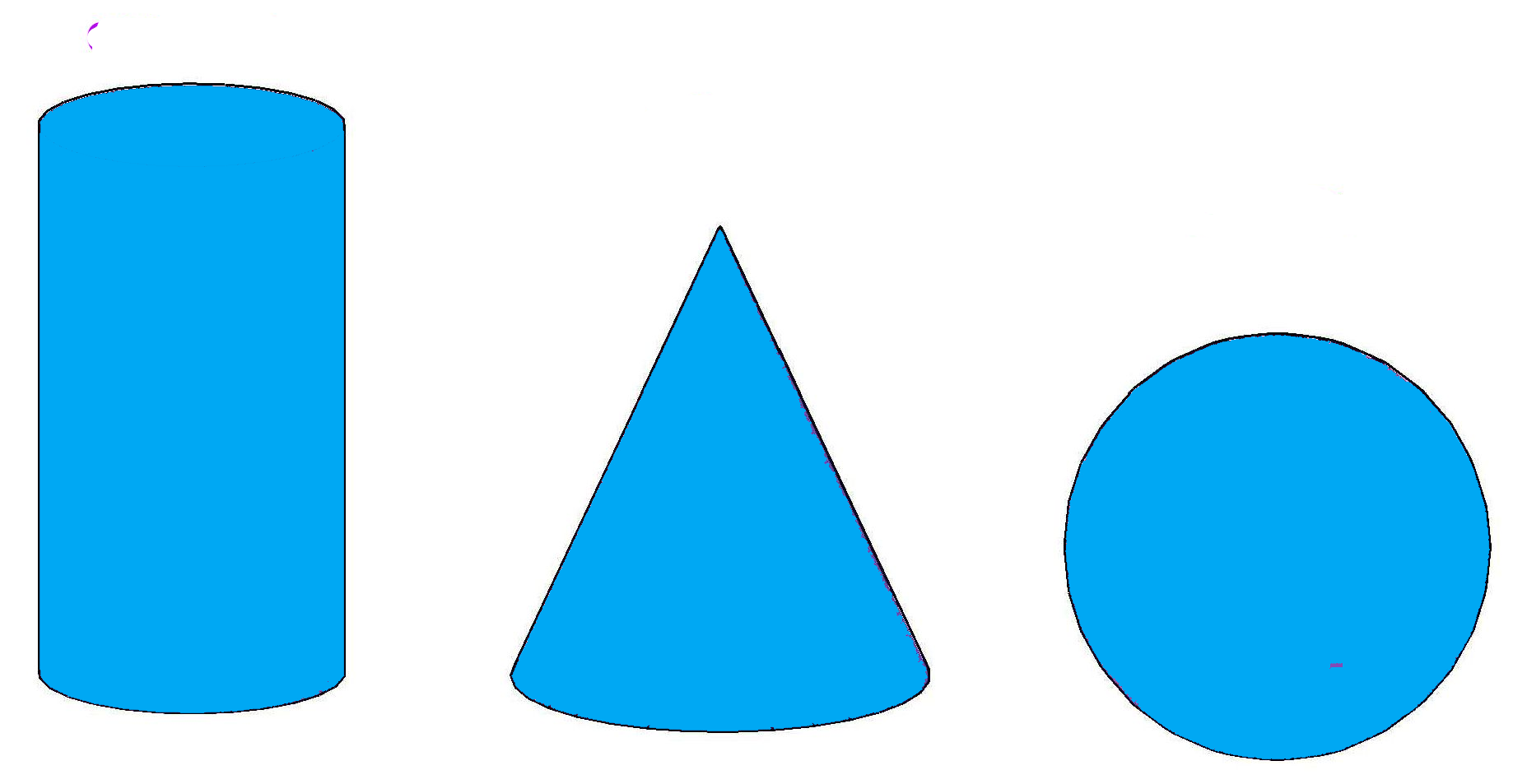
El cono: El cono tiene una cara plana y una superficie curva. Y ¿adivináis que figuras geométrica tiene su cara plana? BINGO, es un círculo.
El cilindro: Tiene una superficie curva al igual que el cono, pero en ese caso dos caras planas y sus caras planas, al igual que el cono, son círculos.
La esfera: En este caso, toda la superficie de la esfera es curva.
Cuerpos geométricos con con todas las caras planas.
El cubo: Este cuerpo geométrico tiene todas sus caras planas. Y todas sus caras planas son cuadrados. Tiene 6 caras, 8 vértices y 12 aristas.
El prisma cuadrangular: Este cuerpo geométrico tiene todas sus caras planas. Dos de sus caras planas son cuadrados y las otras cuatro son rectángulos. Tiene 6 caras, 8 vértices y 12 aristas.
El prisma rectangular: Este cuerpo geométrico tiene todas sus caras planas. Todas sus caras son rectángulos. Tiene 6 caras, 8 vértices y 12 aristas.
La pirámide triangular: Este cuerpo geométrico tiene todas sus caras planas. Todas sus caras son triángulos. Tiene 4 caras, 4 vértices y 6 aristas.
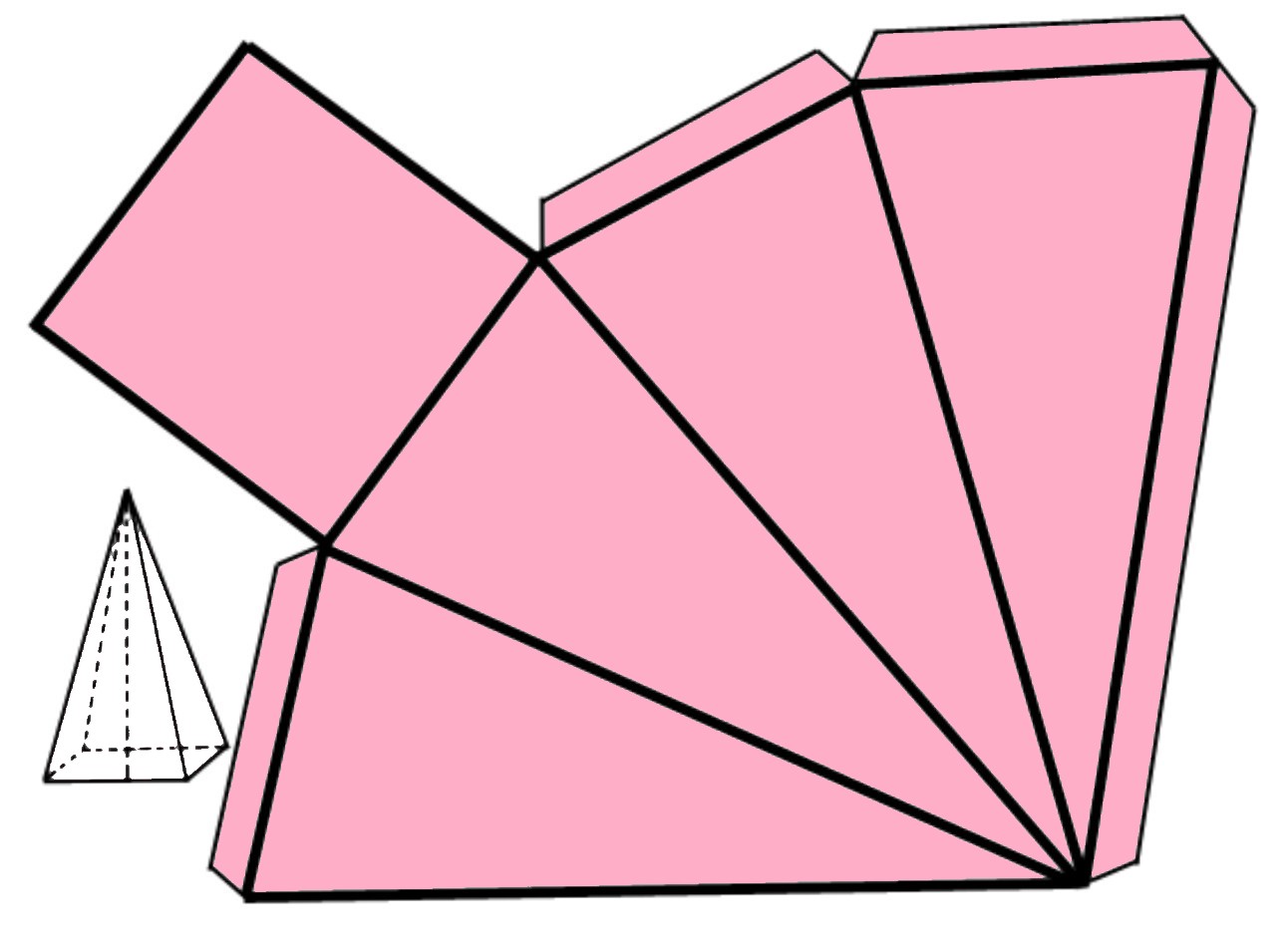
La pirámide cuadrangular: Este cuerpo geométrico tiene todas sus caras planas. Cuatro de sus caras son triángulos y una de ellas es un cuadrado. Tiene 5 caras, 5 vértices y 8 aristas.
Podría hablaros de muchos más cuerpos geométricos, pero en la mayoría de sus casos, estaríamos hablando de prismas o pirámides con distintos números de caras.
Jugando con los Cuerpos Geométricos
Si hay una cosa que he aprendido en todos estos años de experiencia, es que los conceptos nuevos, si se enseñan manipulando y jugando, se aprenden y recuerdan en un futuro con muchísima más facilidad.
Por ellos, os traigo aquí dos juegos para que podáis disfrutar de ellos en vuestras clases o en casa.
Para uno solo necesitarás papeles, tijeras y pegamento y para el otro plastilina y palillos ¿Intrigado?

Descárgate los siguientes PDF y descubre de qué hablo.
CONSTRUYENDO CUERPOS GEOMÉTRICOS DE PAPEL CON COLOR
CONSTRUYENDO CUERPOS GEOMÉTRICOS DE PAPEL PARA COLOREAR
CONSTRUYENDO CUERPOS GEOMÉTRICOS CON PALILLOS Y PLASTILINA